Llama2 with bfloat16 on the SX-Aurora Vector Engine

Llama2 with bfloat16 on the Vector Engine

Erich Focht

This post describes work that builds on and extends the initial port of llama2.c to the VE as described in Llama2 on the SX-Aurora Vector Engine. In that article I showed that two quite simple code changes enable the SX-Aurora VE to run the llama2-7B model with fp32 weights natively with quite impressive performance:


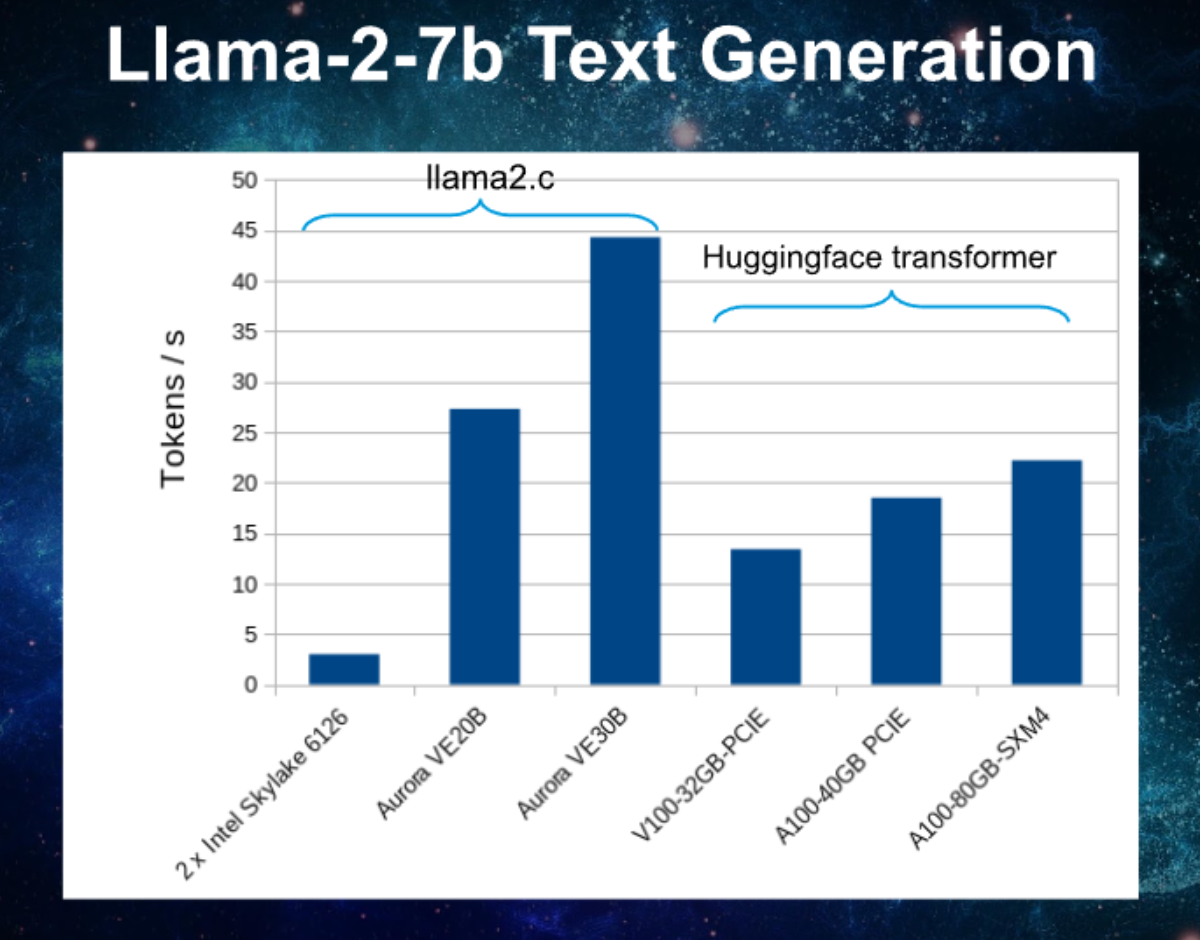
Figure 1: Llama2-7B inference performance on x86_64, VE (fp32) with llama2.c and on GPUs with the transformers library and bfloat16 weights.

The Vector Engine (VE) generations 1 and 2 support only fp32 and fp64 floating point formats, therefore their 48GB HBM2 memory can only accommodate the 7B models which use around 28GB RAM. Being able to run any 16 bit floating point format would enable us to run 13B models on these accelerators.

fp32 versus fp16 versus bfloat16

The single precision 32 bit floating point format defined by IEEE 754 is represented by 1 sign bit, 8 bit exponent and 23 bits mantissa, as depicted in the image below:


Figure 2: 32 bit floating point number example, picture from Wikipedia.

Half-precision floating point numbers (fp16) have 10 bits for mantissa and only 5 bits for the exponent. The bfloat16 format (brain floating point) uses 7 bits for the mantissa and 8 bits for the exponent. fp16 has an advantage in the precision which bfloat16 can represent wider ranges of numbers. The dynamic range of bfloat16 and fp32 is equivalent. The following picture from the TPU docs summarizes the representations:


Figure 3: Bit layout of bfloat16, fp32 and fp16 floating point formats.

The VE has vector-FMAs (fused multiply-add units) capable of operating on vectors of up to 256 fp64, 256 fp32 numbers, or, in packed mode, 512 fp32 numbers. It can not execute operations on fp16 or bfloat16 numbers. Nevertheless, we can use the fp32 execution units to process 16 bit floating point numbers by converting them and shifting them into the right place. The representation in the previous picture shows that bfloat16 and fp32 have the same exponent size while having differently sized mantissa. This means that we can simply load a bfloat16 number into the fp32 register (left aligned) and fill the missing bits of the mantissa with zeros. Or ignore them, as the bfloat16 would anyway deliver less precision than the fp32.

bfloat16 weights

In llama2.c the weights are by default stored in fp32. The most space and compute time is taken by the weights which are used in matrix-vector multiplications. These are the ones which have been stored as bfloat16 for the VE. From the various weight tensors in the model we have left the token_embedding_table and the three rms_*_weight tensors in fp32 format and stored wq, wk, wv, wo, w1, w2, w3 and the (optional) output classifier wcls in bfloat16 by modifying the export.py function.

The first change for bfloat16 weights and the corresponding matrix multiplication was done generically, supporting any processor, and was submitted as a pull request to the upstream repository.

For the Vector Engine we prepared two formats of the weight matrices. llama2.c needs the large language model checkpoint in a special format that is easy to load and map in the C program. The export.py program supports various checkpoint formats (model checkpoints, meta llama and huggingface). The exported binary format is selected with the option --version, the two formats were added for bfloat16 support:

--version -1 : legacy llama2.c format with weight matrix data stored in bfloat16 format. The matrices are left in row-memory-order.
--version -2 . legacy llama2.c format with weight matrix data stored in bfloat16 format and column-memory-order (transposed). This format requires a different matrix-vector multiplication function compared to the original llama2.c.

Example: export meta-llama Llama 2 7B model to bf16 format

python export.py --version -1 --meta-llama ../Llama-2-7b Llama-2-7b.bf16.bin

Example: export meta-llama Llama 2 13B chat model to bf16 format with column memory order matrices:

python export.py --version -2 --meta-llama ../Llama-2-13b-chat Llama-2-13b-chat.bf16.cmo.bin

These exports take around 10 minutes.

Matrix-vector multiply with bfloat16 weights

The original llama2.c matrix-vector multiplication function is simple and implies that the dense matrix is stored in row memory order:

void matmul(float* xout, float* x, float* w, int n, int d) {
    int i;
    #pragma omp parallel for private(i)
    for (i = 0; i < d; i++) {
        float val = 0.0f;
        for (int j = 0; j < n; j++) {
            val += w[i * n + j] * x[j];
        }
        xout[i] = val;
    }
}

The change mentioned in the pull request introducing bfloat16 support can be found in the branch bf16 in this repository. For arbitrary (little endian) processors the modified matrix multiplication uses a union of long and float arrays union lfloat and loads two bfloat16 matrix elements at once which it shifts to the right positions for two consecutive 32 bit float elements. The matrix-vector multiply is strip-mined with the strip size of 64, converts a block of 64 bfloat16 matrix elements into 64 floats and then does the matrix-vecto rproduct in fp32.

void matmul_bf16(float* xout, float* x, bf16* w, int n, int d) {
    int i;
    #define STRIPESZ 64
    union lfloat {
        unsigned long l[STRIPESZ/2];
        float f[STRIPESZ];
    };
    #pragma omp parallel for private(i)
    for (i = 0; i < d; i++) {
        float val = 0.0f;
        union lfloat uf;
        for (int j = 0; j < n; j+=STRIPESZ) {
            for (int k = 0; k < STRIPESZ && (j+k) < n; k+=2) {
                unsigned long wi = *(unsigned int *)(w + i * n + j + k);
                unsigned long wv = (wi & 0xffff0000) << 32;
                unsigned long wr = (wi & 0x0000ffff) << 16;
                uf.l[k / 2] = wv | wr;
            }
            for (int k = 0; k < STRIPESZ && (j+k) < n; k++) {
                val += uf.f[k] * x[j + k];
            }
        }
        xout[i] = val;
    }
}

This is certainly further optimizable, the first target of the exercise was to check if we get reasonable results and the format conversion works properly.

The performance achieved with this approach on a 12 core Intel Skylake Gold 6126 at 2.6GHz is 1.3 tokens/s. A comparable test on the original fp32 code delivers 2.3 tokens/s, obviously the format conversion costs performance and the benefit of loading less data is destroyed by the operations for converting the data.

bfloat16 for Vector Engine

For maximising performance while keepig the code readable I used LLVM intrinsics which map vector instructions into the C language.

The code block for loading up to 512 bfloat16 matrix weights into a packed fp32 vector register is below:

   __vr bf16mskl = _vel_vbrdl_vsl(0x00000000ffff0000, VLEN);
   __vr wv = _vel_vldunc_vssl(4, (void *)(wp), VLEN);
   __vr wr = _vel_vsrl_vvsl(wv, 16, VLEN);
   wr = _vel_vand_vvvl(wr, bf16mskl, VLEN);
   wv = _vel_vor_vvvl(wv, wr, VLEN);

Line 1 broadcasts (vbrdl) the value 0x00000000ffff0000 into each of the 256 slots of a vector register. This value is used later to mask out the lower bfloat16 value.

Line 2 loads 256 consecutive 32bit values from the weight matrix. Each of the 32 bit values is loaded into the upper 32 bits of each 64 bit slot of the vector register wv. The intrinsic’s mnemonic is vldu: vector load upper, and the stride is 4 bytes. Now each slot’s upper 32 bits contains two bfloat16 values, one in the bits 48 to 63, the other in the bits 32 to 47.

Line 3 and 4 creates a new vector register wr by shifting each 64 bit slot of wv 16 bits to the right (vsrl), thus pushing the lower bfloat16 into the bits 16 to 31, and masking all other bits out by a vector AND (vand) operation. Now wr has the lower fp32 value in each 64 bit slot set to the lower bfloat16 value.

Finally line 5 ORs wv and wr together, leaving us with the upper bfloat16 value in the upper 32 bit packed slot and the lower bfloat16 value in the lower 32 bit packed slot. The mantissa of the upper fp32 value is “contaminated” by the lower bfloat16 bits, which we ignore.

The code for the single core dense matrix-vector multiplication without unrolling looks like this:

   #define VLEN (256)
   void sgemv_packed_bf16(float *y, float *x, bf16 *w, int n, int d) {
       int i;
       float zero[2] = {0.0f, 0.0f};
       __vr bf16mskl = _vel_vbrdl_vsl(0x00000000ffff0000, VLEN);
       __vr low32msk = _vel_vbrdl_vsl(0x00000000ffffffff, VLEN);
       for (i = 0; i < d; i++) {
           __vr xv, xlv;
           __vr wv;
           __vr tv1 = _vel_vld_vssl(0, &zero[0], VLEN);
           bf16 *wp = w + i * n;
           for (int j = 0; j < n; j += 2*VLEN) {
               const int vl = n - j < 2*VLEN ? (n - j)>>1 : VLEN;
               if ((unsigned long)(x+j) & 0x7) {
                   xv = _vel_vldu_vssl(8, (void *)(x + j + 1), vl);
                   xlv = _vel_vldlzx_vssl(8, (void *)(x + j), vl);
                   xv = _vel_pvor_vvvl(xv, xlv, vl);
               } else {
                   xv = _vel_vld_vssl(8, (void *)(x + j), vl);
               }
               load_bf16_to_packed_fp32(wv,wp+j,vl);
               tv = _vel_pvfmad_vvvvl(tv, xv, wv, vl);
           }
           sumup_packed_fp32_store(tv,y[i],VLEN);        
       }

Some comments on the code: Line 10 prepares a vector containing zeros by vector-loading with stride 0. The loop over j (line 12) is strip-mined in steps of 512. Lines 14 - 20 load the packed x vector and handle the case that it is not 8-byte aligned. Line 21 loads up to 512 bfloat16 matrix w values as explained in the previous section. Line 22 does a packed vector fused multiply-add (pvfmad) in fp32, up to 512 times tv[k] = tv[k] + wv[k] * xv[k]. Finally line 24 is the reduction summing up all elements in the packed tv vector and storing the result into y[i].

For optimization I unrolled the i loop 16 times, the vector engine benefits of this and can handle it because it has 64 vector registers and can do register renaming in the VPU. The code is available in the github repository https://github.com/efocht/sgemv-intrinsics.

On the VE3 (third generation vector engine) I could not use any intrinsics optimization. Instead I used the original matmul function with 8-fold outerloop (loop over i) unroll. The function is also in the sgemv-intrinsics repository, here.

Column memory order weight matrix

In row memory order the elementwise product of a row and the x vector needs to be reduced, i.e. summed up at the end. The Vector Engine does not support the reduction of a packed vector with up to 512 elements therefore we need to copy the packed vector register, shift the lower 32 bits of each slot up and add the lower and upper parts, then do a 256 elements reduction. The impact of these operations should not be to large as it happens outside the innermost loop. Still, I was curious to see if doing an “outer” multiplication chaged the performance.

Instead of the original “inner” matrix-vector product I use the “outer” product form:

void matmul_cmo(float *y, float *x, float *w, int n, int d) {
    for (int i = 0; i < d; i++)
        y[i] = 0.0f;
    for (int j = 0; j < n; j++) {
        float tmp = x[j];
        for (int i = 0; i < d; i++) {
            y[i] += w[j * d + i] * tmp;
        }
    }
}

This implies that the weight matrix w is stored in column memory order, such that stride 1 accesses are along the columns, not the rows. This formulation avoids the reduction of the elements, multiplies the matrix element with a constant in the innermost, vectorized loop, but has to store the result into the result vector y.

OpenMP parallelization of this function was done over the i loops, i.e. along the column length. Unrolling had almost no impact, therefore the optimized function called for each thread was just:

typedef union {
    float f[2];
    unsigned long u;
} packed_fp32;

void sgemv_bf16_cmo(float *y, float *x, bf16 *w, int n, int d, int nd) {
    float zero[2] = {0.0f, 0.0f};
    __vr wv;
    __vr bf16mskl = _vel_vbrdl_vsl(0x00000000ffff0000, VLEN);
    packed_fp32 pf;

    for (int i = 0; i < nd; i += 2*VLEN) {
        const int vl = nd - i < 2*VLEN ? (nd - i)>>1 : VLEN;
        __vr yt = _vel_vld_vssl(0, &zero[0], vl);
        bf16 *wp = w + i;
        for (int j = 0; j < n; j++) {
            pf.f[0] = pf.f[1] = x[j];
            load_bf16_to_packed_fp32(wv, wp, vl);
            yt = _vel_pvfmad_vvsvl(yt, pf.u, wv, vl);
            wp += d;
        }
        _vel_vstunc_vssl(yt, 8, (void *)(y+i+1), vl);
        _vel_vstlnc_vssl(yt, 8, (void *)(y+i), vl);
    }
}

On the 3rd generation Vector Engine (VE3) has the capability to directly load bfloat16 data and convert it on the fly to fp32. Since the VE3 ISA canges have not been published, yet, I can not do low level optimizations with intrinsics for it. Instead I simply use the unoptimized pure C version matmul_cmo() and replace the function header with

void matmul_ve3_cmo(float *y, float *x, __fp16 *w, int n)

and compile it (basically) with

ncc -O3 -march=ve3 -mfp16-format=bfloat -c matmul_ve3_cmo.c

Performance evaluation

The performance was evaluated on a VE20B vector engine which has a peak memory bandwidth of 1.55 TB/s and a peak single precision performance of 4.91 TFLOPS on 8 cores, as well as on a VE30B with peak memory bandwidth of 2.45 TB/s and 9.83 TFLOPS on 16 cores.

Testing was done with Llama-2-7b being asked to complete the text “The solar system is”. The number of generated tokens was set to 100, 200, 300, 400, 500 and I plotted the “tokens / second” value printed by llama2.c at the end. Temperature was fixed to 0.7 and every test used the same random seed. A sample output is below:

$ ./ve-runbf16 Llama-2-7b.bf16.bin -t 0.7 -s 1234 -n 100 -i "The solar system is"
The solar system is composed of the Sun, the planets, and the objects that orbit the Sun, including
the dwarf planets, the moons of the planets, the asteroids, and the comets. 
The solar system is a part of the Milky Way galaxy, which is itself a part of the Local Group of
galaxies, which is a part of the Laniakea Supercluster, which is a part of the Virgo Supercluster.
The solar 
achieved tok/s: 60.698958


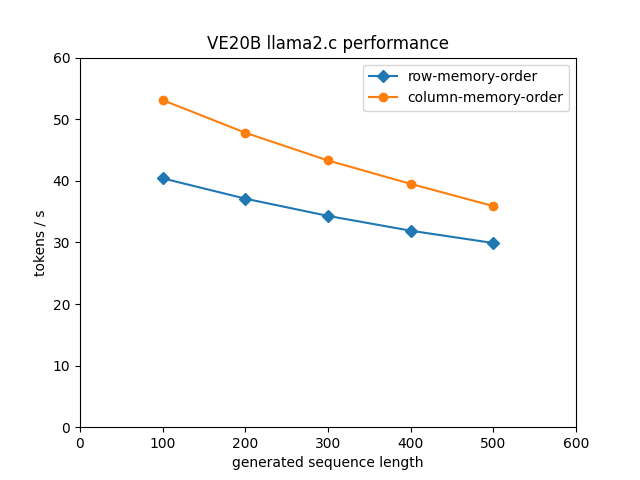
Figure 4: LLM performance with Llama2-7b on Vector Engine VE20B with weight matrices in bfloat16.

Figure 4 shows the performance on the VE20B Vector Engine. The performance is pretty remarcable bearing in mind that the VE does not support bfloat16 and we’re executing the arithmetic operations in fp32 vector units. In a previous post we’ve seen that with 32 it weights in fp32 we reach 27 tokens/s on a VE20B (see figure 1). That result was obtained with a sequence length of 200 and compares to 37.1 tokens/s in bfloat16 (figure 4, row-memory-order). When using column memory order we even reach 47.8 tokens/s for sequence length 200 in bfloat16! The vectorized format conversion and represents a relatively low overhead and we reach more than double the performance of an A100 running with the transformers library on bfloat16 weights.

Running on the last generation vector engine VE30B delivers quite interesting results, shown in figure 5. The best performance is achieved with the same code that was built and compiled for the VE20B (that is code for VE1 and VE2). The intrinsics-optimized code achieves performances of well above 50 tokens/s, even exceeding 60 tokens/s. Interestingly the column-memory-order result for VE30B is worse than the row-memory-order one, opposite to what we saw on VE20B. The reason for this is that we OpenMP parallelize over the cores in i direction, which is the “height” of the matrix and the length of the result vector. Some of the matrices are not large enough such that the average vector length on 16 cores (VE3) is only 145, while the average vector length on 8 cores is in the range of 250.


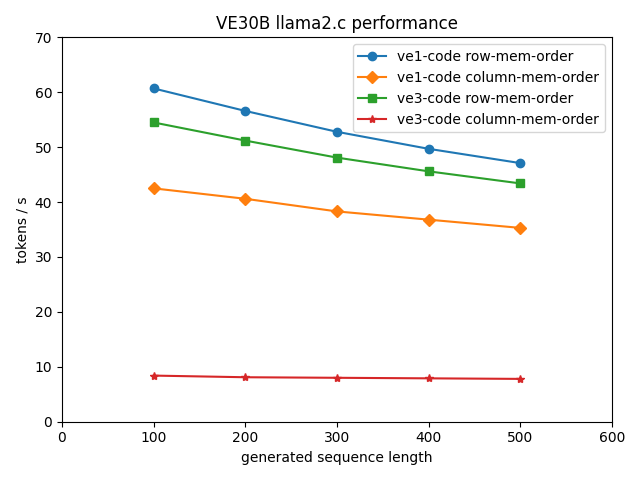Figure 5: LLM performance with Llama2-7b on Vector Engine VE20B with weight matrices in bfloat16.

The VE30B is supporting to some extent the loading of bfloat16 and fp16 data while still using fp32 arithmetic units. Since we don’t have intrinsics support for the VE3, yet, the VE3 specific codes are entirely written in C and only moderately optimized. The green curve in figure 5 (row-memory-order, VE3 code) has its data point for sequence length 200 at 51.2 tokens/s, which is better than the fp32 result from figure 1 (44 tokens/s), but the VE1 intrinsics code is faster with 56.6 tokens/s.

The column-memory-order VE3 result is disappointing, 8 tokens/s are far below expectations and far below the optimized VE1 code.

Conclusion

Emulating bfloat16 with relatively simple vectorizing code for matrix-vector multiplication in llama2.c on the NEC SX-Aurora Vector Engine leads to

reduction of memory demand by almost a factor of two compared to the original fp32 implementation, thus enabling one VE to run eg. Llama-2-13b models,
increase in token generation performance due to reduced demand for memory bandwidth, reaching O(50) tokens/s.

This makes the old VE1 and VE2 accelerators very interesting for on-premise, private LLMs.

The latest generation Vector Engine VE3 can fit even larger models like Llama-2-32b onto one accelerator using bfloat16 and reaches O(60) tokens/s performance.

References and links: